【人気ダウンロード！】 x y/2=4 x/3 2y=5 by cross multiplication method 272610

Solve the following system of equations using the cross multiplication method,axby=ab;bxay=ab Math When you solve the system shown by the elimination method, which statement is true?21x – 3y = 10 represents two lines which are4 Solve the belowmentioned simultaneous linear equations by the method of crossmultiplication (i) 2x y = 4, x y = 6 (ii) 4x 3y = 7, 3x y = 4

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

X y/2=4 x/3 2y=5 by cross multiplication method

X y/2=4 x/3 2y=5 by cross multiplication method-Class 10 Maths MCQs Chapter 3 Pair of Linear Equations in Two Variables 1 A pair of linear equations a 1 x b 1 y c 1 = 0;3x ky 15 = 0 has (i) unique solution (ii) no solution 4 For what value of k, the following system of equations have (i) a unique solution, (ii) no solutions kx 2y = 5;

Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy

Subtract 2y from both sides Subtract 2 y from both sides 3x=42y 3 x = 4 − 2 y Divide both sides by 3 Divide both sides by 3 \frac {3x} {3}=\frac {42y} {3} 3 3 x = 3 4 − 2 y Dividing by 3 undoes the multiplication by 33x 4y = 10 5 Find the value of a and b for which the following system of linear equations has infinite numbers of solutions 2x 3y = 7 x > 3, y < 2 implies ( − 1) y > − 2 which is equal to ( − 2) y > ( − 4) Hence we get x 2 − 2 y > 9 − 4 = 5 As a slightly extended version of Michael Rozenberg 's answer, this can very simply be written down as In my opinion, this proof is the most direct reflection of

Method 1 Solve the two equations simultaneously and yield answer Method 2 Trial and error method Each time it is not feasible to do complete calculations in short span of time For the first equation 40/ (x/y) 2/ (xy)=5 we can predict that 41=5This calculator can be used to expand and simplify any polynomial expressionSolve each of the following systems of equations by the method of cross multiplication 2/x 3/y = 13 5/x 4/y = 2 where x ≠ 0 and y ≠ 0 asked Apr 27 in Linear Equations by Gargi01 (

Solve the following system of equations by using the method of crossmultiplication 2xy3=0,quad 4 2xy=72y 5yx=54x If (x, y) is a solution to the above system of equations, what isFinally, I assume that the "multiplication method" is the same as the method I was taught to call the "addition/subtraction method" With these four assumptions, the answer is, Yes Any linear system of #n# equations in #n# variables can be solved by this method #axby=c# #dxey=f# Mutiply the first equation by #d# and the second by #a# to get Stepbystep explanation The given equation is and Now, multiply first equation by 3 and then add the second equation, we get ⇒ ⇒ ⇒ Squaring on both sides, we get Now, substituting the value of x=4 in the first equation, we get

Solve The Following Systems Of Equations 2 X 3 Y 9 Xy 4 X 9 Y 21 Xy Where X 0 Y 0 Sarthaks Econnect Largest Online Education Community

Find The Equation Of The Plane That Passes Through The Line Of Intersection Of The Planes Mathematics Stack Exchange

Steps for Solving Linear Equation x2y=4 x − 2 y = 4 Subtract x from both sides Subtract x from both sides 2y=4x − 2 y = 4 − x Divide both sides by 2 Divide both sides by − 2 (iii) Method of cross multiplication In this method, we first find the value of one variable (y) in terms of another variable (x) from one equation Substitute this value of y in the second equation Second equation becomes a linear equation in x only and it can be solved for x0 votes 1 answer

Cross Multiplication Method For Solving Equations A Plus Topper

X Y 6 X Y 2 By Elimination Method Novocom Top

A small request to one who has posted the question "always check thoroughly for any typographical errors before posting your questions otherwise, people tend to get confused there are a lot of errors in typing in the question 'hope you know thaUnlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard ExamplesRD Sharma Solutions for Class 10 Chapter 3 Pair Of Linear Equations In Two Variables explains the solution of a system of linear equations in two variables, its graphical and algebraic methods of solving These solutions will help you in excel your 2122 exams

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

Coss Multiplication Method For Solving Linear Equations Ncert 10

Best answer \(\frac{x}{3}\)\(\frac{y}{4}\) = 11 ⇒ 4x 3y = 132 \(\frac{5x}{6}\) \(\frac{y}{3}\) = 7 ⇒ 5x – 2y = 42 Multiplying eq1 by 2 and eq2 by 3 and adding them ⇒ 8x 6y 15x – 6y = 264 – 126 ⇒ 23x = 138 ⇒ x = 6Graph y=2(x3)^24 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Multiply by Simplify by adding and subtracting Tap for more steps Subtract from Add and The final answer is The value at is3/x 1/y = 8 3y x = 8xy 3y 8xy = x y( 3 8x) = x y = x/3 8x 2/x 3/y = 2 2y 3x = 2xy 2 ( x/3 8x) 3x = 2x( x/3 8x) taking LCM 2x 9x 24x square = 2x sq 11x = 22x square x = 0, 11 = 22x;

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4

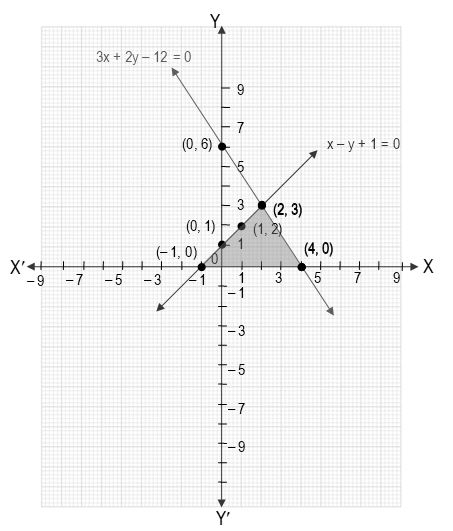
Pair Of Linear Equations In Two Variables

Algebra Graph y=4x y = 4x y = 4 x Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x b m = 4 m = 4RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations In Two Variables Exercise 32 The knowledge of the construction of graphs of linear equations in solving systems of simultaneous linear equations in two variables is practised in this exercise The RD Sharma Solutions Class 10 can be a great help for students for 13x – (–9) = 48 ⇒ 13x = 39 ⇒ x = 3 ∴ Solution is x = 3 and y = – 9 7 For solving pair of equation, in this exercise use the method of elimination by equating coefficients 3 – (x – 5) = y 2 2 (x y) = 4 – 3y Answer 3 – (x – 5) = y 2 ⇒ 3 – x 5 = y 2 ⇒ –x 8 = y 2 ⇒ x

Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths

Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy

Solve each of the following systems of equations by the method of crossmultiplication x 2y 1 = 0 2x 3y 12 = 0 asked Apr 26 in Linear Equations by Haifa (A rational expression is an algebraic expression divided by another algebraic expression such as (3 x2) ÷ (x4) or 3 x2x4 The last fraction is sometimes called a fractional algebraic expression There is a special restriction for all fractions, including fractional algebraic expressions The denominator of the fraction cannot be 01 Solve the following systems of simultaneous linear equations by crossmultiplication method (i) 3x 2y = 4 8x 5y = 9 (ii) 3x – 7y 10 = 0 y – 2x = 3 Solution (i) 3x 2y = 4 8x 5y = 9 We can write it as 3x 2y – 4 = 0 8x 4y – 9 = 0 By cross multiplication method x/ (18 ) = y/ (32 27) = 1/ (15 – 16) By further calculation

Gseb Solutions For Class 10 Mathematics Pairs Of Linear Equations In Two Variables Cbse Tuts

Ex 3 5 1 Which Pair Has Unique No Solution Or Infinitely

44 Solving simultaneous equations (EMA38) Up to now we have solved equations with only one unknown variable When solving for two unknown variables, two equations are required and these equations are known as simultaneous equations(X^22y/x)^10= (X^2)^10 10*1/(1)(x^2)^9*(2y/x)^1 10*9/(1*2)*(x^2)8*(2y/x)^2 10*9/(1*2*3)(x^2)^8 *(2y/x)^3 etc all subsequent terms have the power of yI think you can think this as the sum of x, 2y, x and y Then you arrange them, make them the sum of x, x, 2y and y After, you combine the similar variable, so it'll become xx=2x and 2yy=1y=y, then combine the answer, so it'll become 2xy

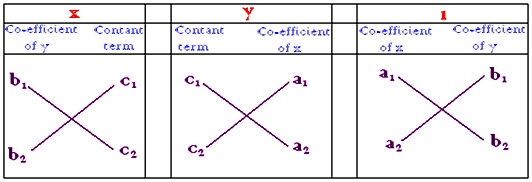
Cross Multiplication Method Formula For Cross Multiplication Linear Equations

X Y 6 X Y 2 By Elimination Method Novocom Top

X y/2 = 4 , x/3 2y = 5 Solving linear equations using cross multiplication method Solving one step equations Solving quadratic equations by factoring Solving quadratic equations by quadratic formula Solving quadratic equations by completing square Nature of the roots of a quadratic equationsSolve the following systems of equations x y/2 = 4 x/3 2y = 5 1 answer Solve each of the following systems of equations by the method of crossmultiplication x/a = y/b ax by = a^2 b^2 asked Apr 27 in Linear Equations by Gargi01 (90k points) pair of linear equations in two variables;Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

無料ダウンロード 3x 2y5 X5 Y

 Using crossmultiplication method, we obtain p – 26 – (– 36) = q – 24 – (– 39) = 1 9 – 4 p 10 = q 15 = 1 5 p 10 = 1 5 and q 15 = 1 5 p = 2 and q = 3 1 x = 2 and y = 1 3 x = 1 2 and y = 1 3 (ii) 2 x 3 y = 2 4 x – 9 y = – 1 Putting 1 x = p and 1 y = q in the given equations, we obtain 2p 3q = 2 _____ (1) 4p – 9q = –1 _____ (2) Multiplying equation (1) by 3, we obtain 6p 9q = 6 _____ 1 Solve the following systems of simultaneous linear equations by crossmultiplication method (i) 3x 2y = 4 8x 5y = 9 (ii) 3x – 7y 10 = 0 y – 2x = 3 Solution (i) 3x 2y = 4 8x 5y = 9 We can write it as 3x 2y – 4 = 0 8x 4y – 9 = 0 By cross multiplication method x/(18 ) = y/(32 27) = 1/(15 – 16) By further calculation Rewrite x2y=4 x2y=5 in column form x2y=4 x2y=5 Because both equations have x 2y on the left and different constants on the right, we know immediately that there is no solution These two lines are parallel and different;

Class Ten Maths Ncert Chapter 3 Solutions Freeguru Helpline

Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths

The sum of the coefficients of y is zero Then, you can solve for x B Section 35 Lagrange Multipliers In the previous section we optimized (ie found the absolute extrema) a function on a region that contained its boundaryFinding potential optimal points in the interior of the region isn't too bad in general, all that we needed to do was find the critical points and plug them into the functionX 2y = 5;

Coss Multiplication Method For Solving Linear Equations Ncert 10

2x 5y 4 And 3x 2y 16 0 Find X And Y Brainly In

The important topics present in NCERT Solutions for Class 10 Maths Chapter 3 are substitution method, elimination method and crossmultiplication method of pair of linear equations in two variables By solving problems based on these concepts students The Questions and Answers of 04x 03y=17 07x02y=08 7(y 3)2(X 2)=14 4(y2) 3(x3)=2 X y/2=4 X/3 2y=5 solve this in two min From substitution, elimination,and cross multiplication method?One way to solve the equation is multiply the first by 2 and then subtract the first equation from the second It will look like this step 1 multiply the first by 2 8x10y=10, and leave the 2nd equation unchanged 3x10y=15 Now add the 2 equati

Solve The Following System Of Equations By Method Of Cross Mult

Solve Using Cross Multiplication Method X Y 72x 3y 11

Free system of equations calculator solve system of equations stepbystepAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy^ {2}4y=5 x 2 − 2 x y 2 − 4 y = − 5 Add 5 to both sides of the equationA 2 x b 2 y c 2 = 0 is said to be inconsistent, if Answer Answer b 2 Graphically, the pair of equations 7x – y = 5;

無料ダウンロード 3x 2y5 X5 Y

How To Solve A B X A B Y 2ab B2 A B X Y B2 By Cross Multiplication Method Studyrankersonline

Steps for Solving Linear Equation x = 2 y 5 x = 2 y − 5 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2y5=x 2 y − 5 = x Add 5 to both sides Add 5 to both sidesSelina Solutions for Class 9 Maths Chapter 6 Simultaneous Equations An equation of the form axbyc=0 is called a linear equation in which a,b and c are constants (real numbers and x and y are variables each with degree 1 (one) The Chapter 6 of class 9 takes the students to the depth of simultaneous linear equations in 2 variables(ii) Elimination Method (iii) Cross multiplication method (Level 1) 1 Find the value of a so that the point(3,9) lies on the line represented by 2x3y=5 Ans a= 2 Find the value of k so that the lines 2x – 3y = 9 and kx9y =18 will be parallel Ans k= 6 3 Find the value of k for which x 2y =5, 3xky15=0 is inconsistent

Solve The Following System Of Equations By Using The Method Of Cro

Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community

Example Using the graphical method, find the solution of the systems of equations y x = 3 y = 4x 2 Solution Draw the two lines graphically and determine the point of intersection from the graph From the graph, the point of intersection is (1, 2)The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically Solution 1 This is the simple way of doing the problem Just solve for y y to get the function in the form that we're used to dealing with and then differentiate y = 1 x ⇒ y ′ = − 1 x 2 y = 1 x ⇒ y ′ = − 1 x 2 So, that's easy enough to do However,

8x 5y 9 3x 2y 4 Solve Using Substitution And Cross Multiplication Method Youtube

Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community

So x2 − 2xy −y2 = x−(1 2 )y The question amounts to showing that the elliptic curve Y^2 = X^2X1, Z^2 = X^2X1 has no rational points other than those with X=0 and X=\infty That can be done by elementary means but The question amounts to showing that the elliptic curve Y 2 = X 2 X 1, Z 2 = X 2 −X 1 has no rationalY 3x = 10 −y − 3x = 10 A You eliminate y;In case there is a unique solution, find it by using cross multiplication method (i) x – 3y – 3 = 0 (ii) 2x y = 5 3x – 9y – 2 = 0 3x 2y = 8

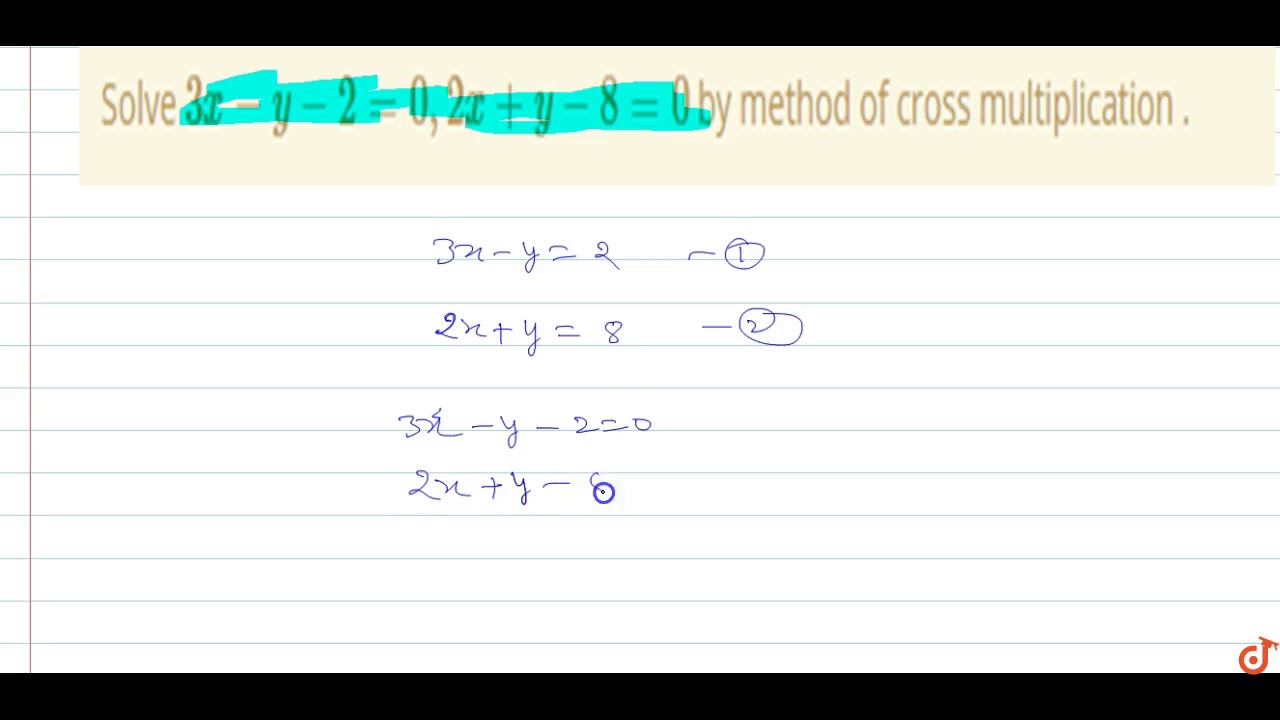
Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube

Linear Systems With Multiplication Algebra Socratic

For example, the equations x 2y = 10 and 3x y = 3 form simultaneous equations Solution A value or set of values that make the simultaneous equations true For example, the solution to the equations 2x 3y = 15 and x y = 10 is x = 3 and y = 7X = 1/2 x = 0, 1/2 If x= 0, y =0 and`x y/2 = 4` (i) `x/3 2y = 5` (ii) From (i), we get `(2x y)/2 = 4` 2x y = 8 y = 8 2x From (ii), we get x 6y = 15 (iii) Substituting y = 8 2x in (iii), we get x 6(8 2x) = 15 `=> x 48 12x = 15` => 11x = 15 48 => 11x = 33 `=> x = (33)/(11) = 3` Putting x = 3 in y = 8 2x we get y = 8 2 x 3 = 8 6 = 2 y = 2

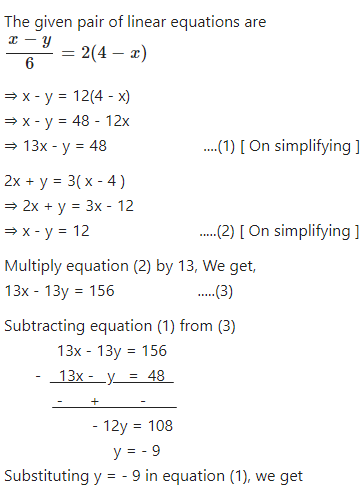
Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp

Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables

Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau

X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top

1

Solve By Using Cross Multiplication Method 3x 4y 10 And 2x 2y 2 Class 10 Brainly In

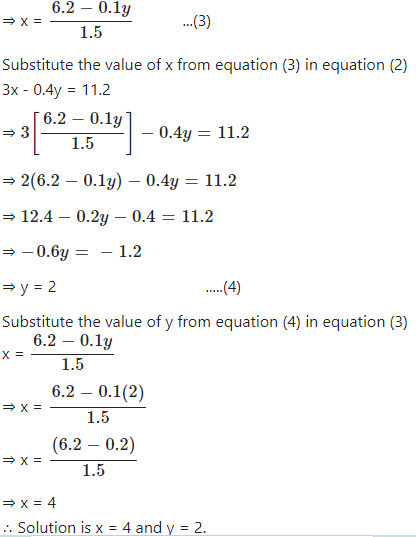
Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp

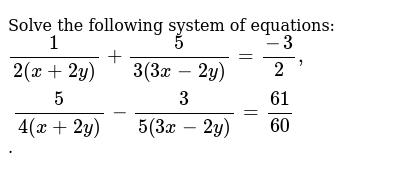
Solve The Following System Of Equations 1 2 X 2y 5 3 3x 2

Chapter Solving Linear Equations 2 Manualzz

Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15

Model Question Ppaer Term1 Grade 9

Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community

Important Questions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables

2x Y 3 0 4x Y 3 0 By Cross Multiplication Novocom Top

1 Solve By Cross Multiplication Method 2x Y 3 0 And 4x Y 3 0 Brainly In

Ex 3 5 3 Solve By Substitution And Cross Multiplication

How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora

Solve The Following Systems Of Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Sarthaks Econnect Largest Online Education Community

100以上 Solve By Substitution Method X Y 14 X Y 4 Solve By Substitution Method X Y 14 X Y 4

Solve The Following Pair Of Equations By Cross Multiplication Method 2x 5y 4 3x 8y 5

Solve This By Cross Multiplication Method 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Mathematics Topperlearning Com K2zyk5cc

How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora

Maths Mania52 Equations Applied Mathematics

Coss Multiplication Method For Solving Linear Equations Ncert 10

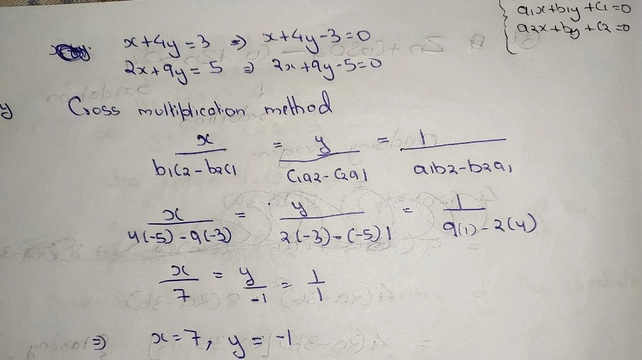
Solve The Equation X4y32x9y5 See How To Solve It At Qanda

Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables

Ncert Solutions Class 10 Maths Ch 3 Pair Of Linear Equations In Two Variables Edu Spot

Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4

Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables

Pair Of Linear Equations In Two Variables Equations Cbse Class 10 Ekshiksha

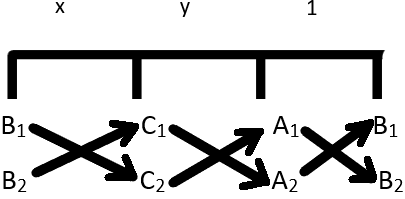
Method Of Cross Multiplication Solve By Method Of Cross Multiplication

100以上 Solve By Substitution Method X Y 14 X Y 4 Solve By Substitution Method X Y 14 X Y 4

Www Topperlearning Com R S Aggarwal And V Aggarwal Solutions Cbse Class 10 Mathematics R S Aggarwal And V Aggarwal Mathematics X Linear Equations In Two Variables

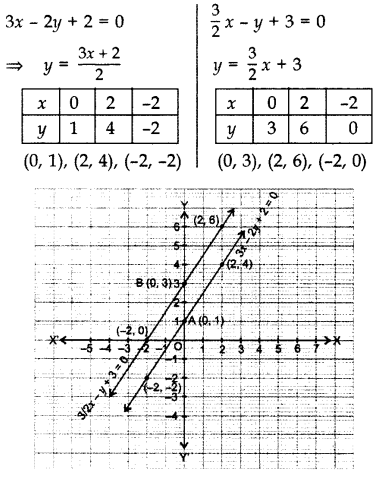
Important Questions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Learn Cbse

Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths

M 10 Chapter 01

How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora

How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4

Coss Multiplication Method For Solving Linear Equations Ncert 10

Solve The Following Pair Of Linear Equation Bycross Multiplication Method X 2y 2 X 3y 7

Q Tbn And9gcsoh2cbqov6kki4tz04fcaup29fu05daqrdet8breolhlkvprlk Usqp Cau

Ex 3 5 3 Solve By Substitution And Cross Multiplication

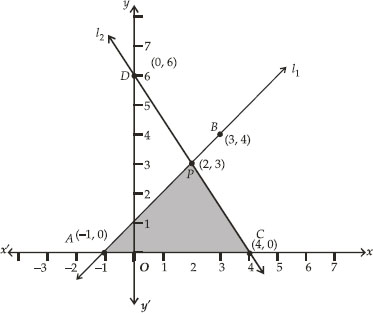
Ncert Solutions Pair Of Linear Equations In Two Variables Class 10

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

Solve The Pair Of Linear Equation By Cross Multiplication Method 5x 4y 4 0 X 12y 0 Brainly In

Cross Multiplication Method For Solving Equations A Plus Topper

Mp Board Class 10th Maths Solutions Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5 Mp Board Solutions

Solve X Y 7 And 3x 2y 11

Solve The Following System Of Equations By Method Of Substitutio

Solve The Pair Of Equations 2 X 3 Y 13 5 X 4 Y 2 Youtube

Maths Class 10 Pages 51 100 Flip Pdf Download Fliphtml5

Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables

Chapter 6 Simultaneous Linear Equations Including Problems Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning

0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question

Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables

How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora

Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Free Study Material Cbse Sample Papers Books Studyguide360

Solve The Following System Of Equations By Method Of Cross Mult

Q Tbn And9gcrumndxcxvoc4aa98ti5lvoli9zrm1ajypkprnjttswbb Pq7ge Usqp Cau

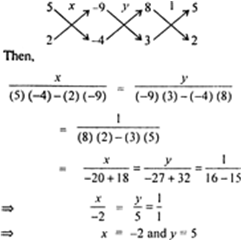
Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4 Zigya

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3

Systems Of Linear Equations

Solve The Following System Of Equations By Method Of Cross Mult

Class Ten Maths Ncert Chapter 3 Solutions Freeguru Helpline

Cbse 10 Math Ncert Solutions

Solve The System Of Eq 2x 3y 17 3x 2y 6 By Method Of Cross Multiplication Brainly In

Solve The Pair Of Linear Equations By Cross Multiplication Method 2 2x Y 5 3 X 3y 1 0 Brainly In

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

Solve The Following System Of Equation 2x 3y 8 0 4x 5y 14 0

Ex 3 5 3 Solve By Substitution And Cross Multiplication

Find The Value Of X And Y Using Cross Multiplication Method 4x 3y 8 And 6x 5y 13